문제요약
각 지역은 유일한 번호로 구분
두 지역간 통과 시 걸리는 시간은 모두 1
흩어진 부대원들이 최단시간 내에 부대가 있는 지역으로 복귀하고자 함
단, 경로가 없어져서 복귀 불가능한 대원이 있음
총 지역 수 n, 두 지역 왕복길 정보 roads, 각 부대원 위치 정보 sources, 지역 destination → sources 순서대로 복귀 가능한 최단 시간 배열을 구하고 복귀가 불가능하면 -1로 표기하라
입력
3≤ n ≤ 10^5
(각 지역 : 정수 1부터 n까지 번호로 구분)
2≤roads [[a,b], …] 2차원 배열 ≤ 5*10^5
([a,b] : a, b가 왕복가능)
1≤sources≤5*10^2
1≤destination≤n
출력
return int[]
어떻게 풀까?
- 다른 지역에 있는 부대원들이 모두 부대가 있는 한 지역으로 최단 시간 내에 가야함 ⇒ 거꾸로 생각해보면, 한 지점에서 모든 지점으로 가야함 ⇒ 다익스트라 문제 ⇒ 다익스트라의 시간복잡도는 O(nlogn)이므로 가능
- 다익스트라로 모든 지역에서 부대 복귀하는 최단distance 구한 뒤, sources를 돌아가면서 해당하는 distance 값을 answer 배열에 넣기 (단, 무한대(불가능)일 경우, -1 넣기)
- 지역번호는 1부터 n인 점 유의!
내 코드
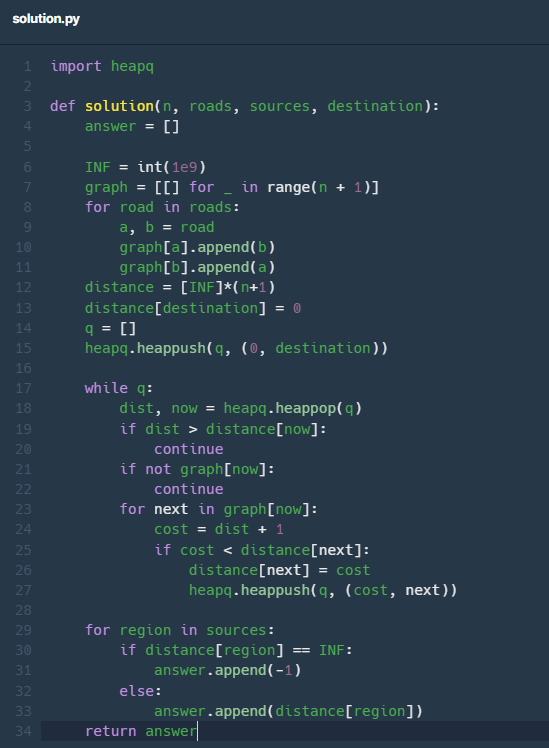
import heapq
def solution(n, roads, sources, destination):
answer = []
INF = int(1e9)
graph = [[] for _ in range(n + 1)]
for road in roads:
a, b = road
graph[a].append(b)
graph[b].append(a)
distance = [INF]*(n+1)
distance[destination] = 0
q = []
heapq.heappush(q, (0, destination))
while q:
dist, now = heapq.heappop(q)
if dist > distance[now]:
continue
if not graph[now]:
continue
for next in graph[now]:
cost = dist + 1
if cost < distance[next]:
distance[next] = cost
heapq.heappush(q, (cost, next))
for region in sources:
if distance[region] == INF:
answer.append(-1)
else:
answer.append(distance[region])
return answer
'알고리즘 문제(Python) > 프로그래머스' 카테고리의 다른 글
| [Lv.3] 미로 탈출 명령어(Python) (0) | 2023.01.08 |
|---|---|
| [Lv.2] 유사 칸토어 비트열(Python) (2) | 2023.01.03 |
| [Lv.2] 마법의 엘리베이터(Python) (0) | 2023.01.02 |
| [Lv.2] 할인 행사(Python) (0) | 2022.12.01 |
| [Lv.2] 두 큐 합 같게 만들기(Python) (0) | 2022.11.30 |