문제요약
n x m 격자 미로
(x, y) → (r, c)로 이동하여 탈출
- 격자 밖으로 나갈 수 없음
- (x, y) → (r, c) 이동거리는 총 k
- (x, y), (r, c) 포함하여 같은 격자 2번 이상 방문 가능
- 탈출경로를 문자열로 나타넀을 때, 사전 순으로 가장 빠른 경로 반환 (d : 아래 1칸, l: 왼쪽 1칸, r: 오른쪽 1칸, u: 위로 1칸)
- 미로탈출 경로를 반환하되, 탈출 못하면 ‘impossible’반환
입력
2 ≤ n ≤ 50
2 ≤ m ≤ 50
1 ≤ x ≤ n
1 ≤ y ≤ m
(x, y) ≠ (r, c)
1≤ k ≤ 5^2*10^2
출력
return str
어떻게 풀까?
- 시간복잡도 : 최대 50x50 크기의 격자이고 한 칸 당 최대 4방향으로 이동이 가능하며, k의 최대 값도 5^2*10^2인데다, 여러 경로가 나올 수 있고 그 중에서 사전 순으로 가장 빠른 경로를 반환해야함
⇒ 단순 BFS로 모든 경우를 산출한 뒤 그 중에서 사전 순으로 가장 빠른 답 반환하면 시간초과 발생 - 사전 순으로 가장 빠르다
⇒ 매번 결정마다 가장 빠른 경로를 큐의 가장 앞에 넣어서 최단경로를 도출 필요
⇒ 다익스트라 활용 가능 - 다익스트라를 활용하더라도, 이 문제의 경우 최단거리가 아닌 k 번 이내 방문에 대한 경로를 도출해내야하고 같은 격자를 여러번 방문할 수 있기 때문에, 이러한 조건들에 대해 별도 처리를 해줌으로써 최대한 시간복잡도를 다익스트라의 시간복잡도에 가깝도록 조치해줄 필요가 있음
- 도착지점에 도착했을 때, 남은 이동가능 횟수가 2의 배수여야함(갔다 돌아오기 (예: d→u, l→r등))
- 다음 지점을 탐색할 때, 해당 지점과 도착지점의 거리가 k보다 크면 어차피 탈출 불가능한 경로임(모두 거리가 1칸이기 때문에 지점 간 거리가 이동거리와 동일함)
내 코드
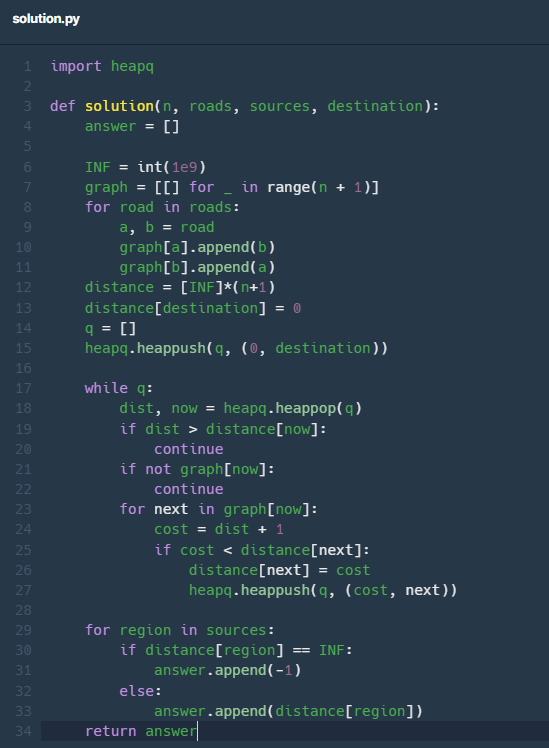
import heapq
def solution(n, m, x, y, r, c, k):
q = []
dr = ['d', 'l', 'r', 'u']
dx = [1, 0, 0, -1]
dy = [0, -1, 1, 0]
heapq.heappush(q, ('', x, y))
while q:
path, x, y = heapq.heappop(q)
if x == r and y == c:
if len(path) == k:
return path
elif (k - len(path)) % 2:
return 'impossible'
for i in range(4):
next_x = x + dx[i]
next_y = y + dy[i]
if next_x <= 0 or next_x > n or next_y <= 0 or next_y > m:
continue
if abs(next_x - r) + abs(next_y - c) + len(path) > k:
continue
heapq.heappush(q, (path+dr[i], next_x, next_y))
return 'impossible'
'알고리즘 문제(Python) > 프로그래머스' 카테고리의 다른 글
| [Lv.3] 부대복귀(Python) (0) | 2023.01.05 |
|---|---|
| [Lv.2] 유사 칸토어 비트열(Python) (2) | 2023.01.03 |
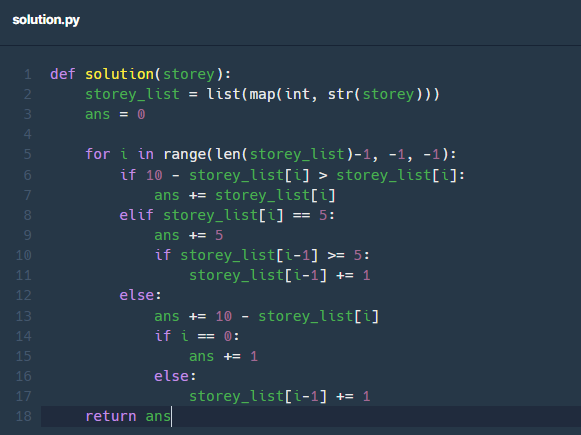
| [Lv.2] 마법의 엘리베이터(Python) (0) | 2023.01.02 |
| [Lv.2] 할인 행사(Python) (0) | 2022.12.01 |
| [Lv.2] 두 큐 합 같게 만들기(Python) (0) | 2022.11.30 |